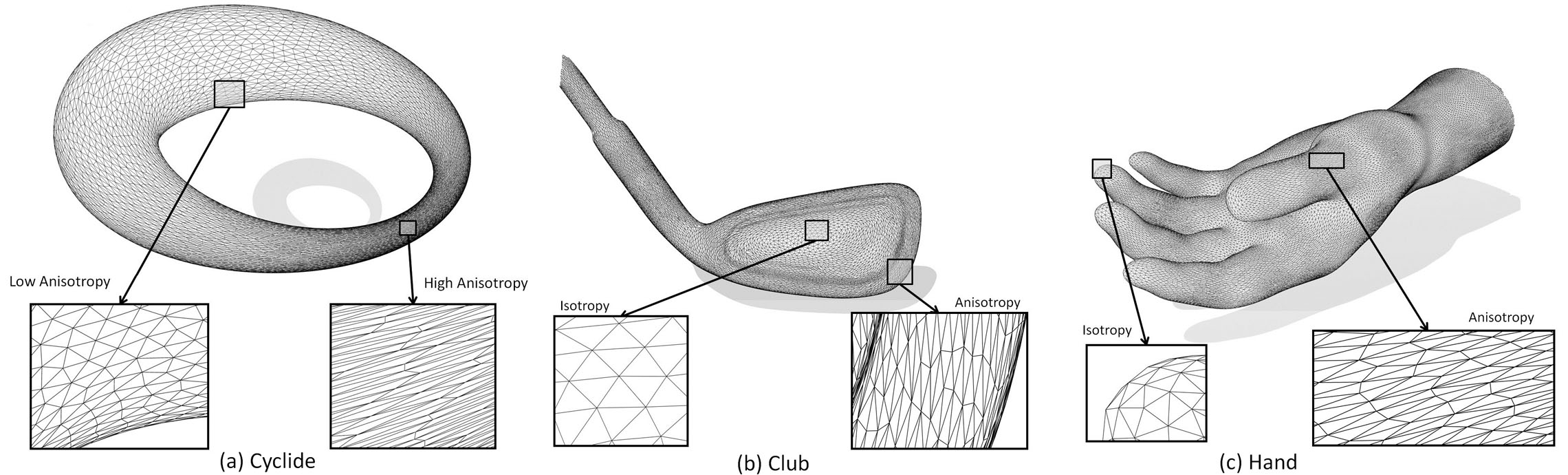
This paper introduces a particle-based approach for anisotropic surface meshing. Given an input polygonal mesh endowed with a Riemannian metric and a specified number of vertices, the method generates a metric-adapted mesh. The main idea consists of mapping the anisotropic space into a higher dimensional isotropic one, called "embedding space". The vertices of the mesh are generated by uniformly sampling the surface in this higher dimensional embedding space, and the sampling is further regularized by optimizing an energy function with a quasi-Newton algorithm. All the computations can be re-expressed in terms of the dot product in the embedding space, and the Jacobian matrices of the mappings that connect different spaces. This transform makes it unnecessary to explicitly represent the coordinates in the embedding space, and also provides all necessary expressions of energy and forces for efficient computations. Through energy optimization, it naturally leads to the desired anisotropic particle distributions in the original space. The triangles are then generated by computing the Restricted Anisotropic Voronoi Diagram and its dual Delaunay triangulation. We compare our results qualitatively and quantitatively with the state-of-the-art in anisotropic surface meshing on several examples, using the standard measurement criteria.